Само название газа - абсолютно полупрозрачный газ /А.Пп. газ/ - говорит о его свойствах. Если в данный промежуток времени А.Ч. тело излучило n квантов и те в свою очередь вызвали возбуждение n молекул А.Пп. газа, то при переходе этих n молекул в невозбужденное состояние n/2 переизлученных квантов будет излучено в направлении А.Ч. тела и поглотится им, а n/2 переизлученных квантов будут продолжать свой дальнейший путь в атмосфере А.Пп. газа в направлении от А.Ч. тела и вновь вызовут возбуждение n/2 молекул и т.д. Далее с каждым переизлучением в направлении от А.Ч. тела будут излучены n/4 кванта, n/8 квантов, n/16 квантов и т.д. Если всего было K переизлучений, то к этому моменту в направлении от А.Ч. тела будет излучено n/2к квантов. Как видно, излучение А.Ч. тела в среде А.Пп. газа происходит по законам, отличным от законов излучения А.Ч. тела в вакууме. Здесь вступают в силу кванто¬вые процессы переизлучения. Суммарная энергия переизлученных квантов, прошедших сквозь среду А.Пп. газа определяется первоначально излученной А.Ч. телом энергией и средним количеством переизлучений первоначально излученного кванта в среде А.Пп. газа. Ниже приведем расчет излучения А.Ч. тела в среде А.Пп. газа.
Возьмем А.Ч. тело радиусом r и нагреем его до температуры T. В начале нашего эксперимента А.Ч. тело /радиуса r и температуры T/ поместим в вакуум и на расстоянии R от центра А.Ч. тела измерим болометрическим датчиком то количество энергии E, которое попадет на единицу поверхности в единицу времени. Полная энергия, излученная А.Ч. телом за единицу времени в окружающее пространство, будет:
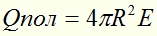
Т.к. площадь поверхности А.Ч. тела равна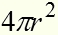 , то энергия, излучаемая единицей площади А.Ч. тела в единицу времени, будет:
, то энергия, излучаемая единицей площади А.Ч. тела в единицу времени, будет:
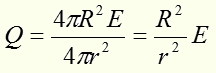
Применяя закон Стефана-Больцмана, измерим температуру А.Ч. тела

Подставляя значение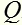 в формулу /2/, получаем температуру T
в формулу /2/, получаем температуру T
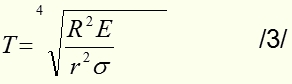
Видоизменим опыт. Пространство на расстоянии R от центра А.Ч. тела заполним А.Пп. газом и посмотрим, какую энергию зарегистрирует болометрический датчик в этом случае. /Расстояние от центра А.Ч.тела до болометрического датчика неизменно остается R/. Но теперь нам надо знать, каково будет среднее количество переизлучений квантов, излученных А.Ч. телом. Каким-то образом нам удалось зарегистрировать среднее количество переизлучений K первоначально излученных квантов в среде А.Пп. газа. Тогда болометрический датчик зарегистрирует энергию в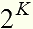 меньшую, чем было зарегистрировано при излучении А.Ч. телом в вакууме. Т.е. болометрический датчик зарегистрирует энергию :
меньшую, чем было зарегистрировано при излучении А.Ч. телом в вакууме. Т.е. болометрический датчик зарегистрирует энергию :
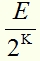
А теперь представим, что эти данные, полученные по показа¬ниям болометрического датчика /болометрических датчиков/, используют в своих исследованиях два экспериментатора, А и Б.
Экспериментатор А знает, что А.Ч. тело окружено А.Пп. газом, а также знает, каким образом А.Ч. тело излучает свою энергию в среде А.Пп. газа.
Экспериментатор Б знает, что А.Ч. тело окружено каким-то газом, но он считает, что этот газ почти не влияет на величину энергии излучения А.Ч. тела. А если как-то влияет, то этой величиной, вследствие того, что она мала /он так думает/, можно пренебречь. Т.е. экспериментатор Б пользуется только законами Планка, Стефана-Больцмана, Вина для излучения А.Ч. тела в вакууме.
Представим себе, что оба экспериментатора снабжены несколькими болометрическими датчиками, регистрирующими энергию квантов во всем диапазоне длин волн, излучаемых А.Ч. телом. Т.е. при помощи этих болометрических датчиков экспериментаторы смогут построить кривую распределения энергии, излучаемой А.Ч. телом в зависимости от длины волны. У обоих экспериментаторов есть прибор угломер. При помощи этого прибора они смогут точно определить угол, под которым наблюдается поверхность А.Ч. тела, а следовательно зная R, могут определить r.
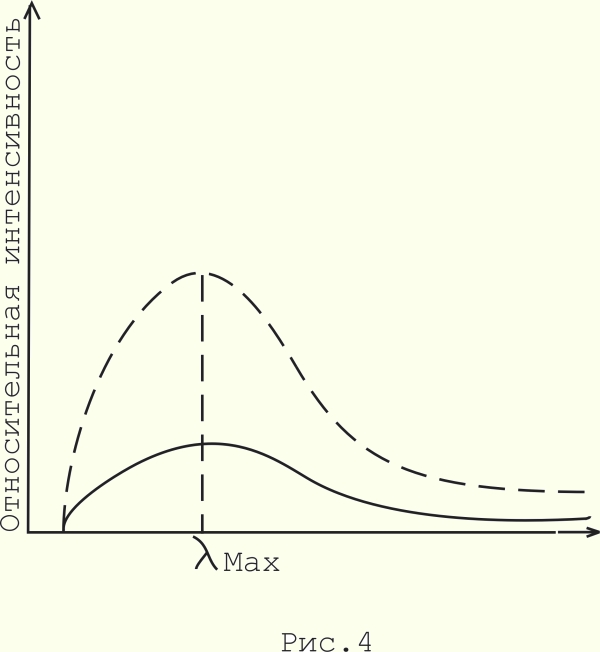
Экспериментатор А начнет с того, что по показаниям болометрических датчиков построит кривую распределения энергии, излучаемой А.Ч. телом в зависимости от длины волны /сплошная кривая см. рис, 4/. Далее из построенного графика он определит максимум этой кривой и найдет λmах. Затем, применив закон Вина Tλmах=2896 мк*град., экспериментатор А определит истинную температуру А.Ч. тела:

После этого по формуле /З/ экспериментатор А определит ту суммарную энергию, которую должны были бы зарегистрировать его болометрические датчики, если бы А.Ч.тело излучало в вакууме.
Подставляя /4/, получаем:
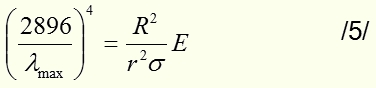
отсюда:
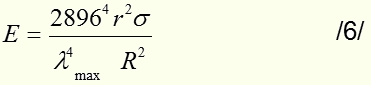
где E - суммарная энергия на единицу площади, которую должны были бы зарегистрировать болометрические датчики, если бы А.Ч. тело излучало в вакууме.
Но болометрические датчики зарегистрировали энергию в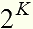 раза меньшую, чем E.
раза меньшую, чем E.
Сравнивая величины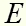 и
и 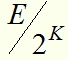 , экспериментатор А определит среднюю величину переизлучений первоначально излученного кванта. Затем экспериментатор А начертит кривую распределения энергии, излучаемой А.Ч. телом в вакууме в зависимости от длины волны /пунктирная кривая см. рис. 4/. Мы видим, что экспериментатор А прекрасно справился со своей задачей. Все данные у него получились в полном согласии с экспериментом.
, экспериментатор А определит среднюю величину переизлучений первоначально излученного кванта. Затем экспериментатор А начертит кривую распределения энергии, излучаемой А.Ч. телом в вакууме в зависимости от длины волны /пунктирная кривая см. рис. 4/. Мы видим, что экспериментатор А прекрасно справился со своей задачей. Все данные у него получились в полном согласии с экспериментом.
Посмотрим, как экспериментатор Б справится с задачей. Все ли у него получится в соответствии с данными эксперимента.
В начале экспериментатор Б поступит так же, как и А. По показаниям болометрических датчиков он построит кривую распределения энергии, излучаемой А.Ч. телом в зависимости от длины волны /сплошная кривая см. рис. 4/. Далее, определив λmах, он по формуле Вина определит температуру Т А.Ч. тела.
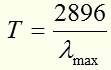
Затем экспериментатор Б решит проверить эти данные температуры по формуле Стефана-Больцмана. Суммарная энергия на единицу поверхности, которую зарегистрируют его болометрические датчики, будет равна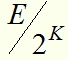 , как и у первого экспериментатора. Определив угломером величину r - радиус А.Ч. тела, экспериментатор Б запишет формулу /5/, но вместо величины E там фактически будет стоять величина
, как и у первого экспериментатора. Определив угломером величину r - радиус А.Ч. тела, экспериментатор Б запишет формулу /5/, но вместо величины E там фактически будет стоять величина
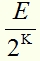
Экспериментатор Б обнаружит, что величина в правой части равенства будет меньше, чем в левой части. И чем больше будет величина K, тем большее несоответствие правой и левой частей уравнения обнаружит экспериментатор Б. Возможно, экспериментатор Б решит, что радиус А.Ч. тела был определен
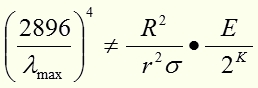
неправильно. А возможно, экспериментатор Б решит, что разница в левой и правой частях уравнения объясняется погрешностью измерения болометрических датчиков. Но применяя более точные приборы, экспериментатор Б придет к тем же необъяснимым результатам.
На основании вышеизложенного примера с экспериментаторами А и Б читатель убедился в том, что если А.Ч. тело излучает свою энергию не в вакууме, а в среде какого-то газа, то надо знать, насколько свойства реального газа, окружающего А.Ч.тело, приближаются к свойствам А.Пп. газа. Пренебрежение свойствами А.Пп. газа может привести к большим ошибкам в исследовании экс-периментальных данных, в чем вы убедились.
Был разобран простейший случай переизлучения А.Пп. газом квантов по всему спектру излучения А.Ч. тела, когда попавший в молекулу А.Пп. газа квант переизлучился в точно такой же квант. Но, как известно, в природе существует и более сложный способ переизлучения. Для примера обратимся к спектру атома водорода /см. рис.5/.
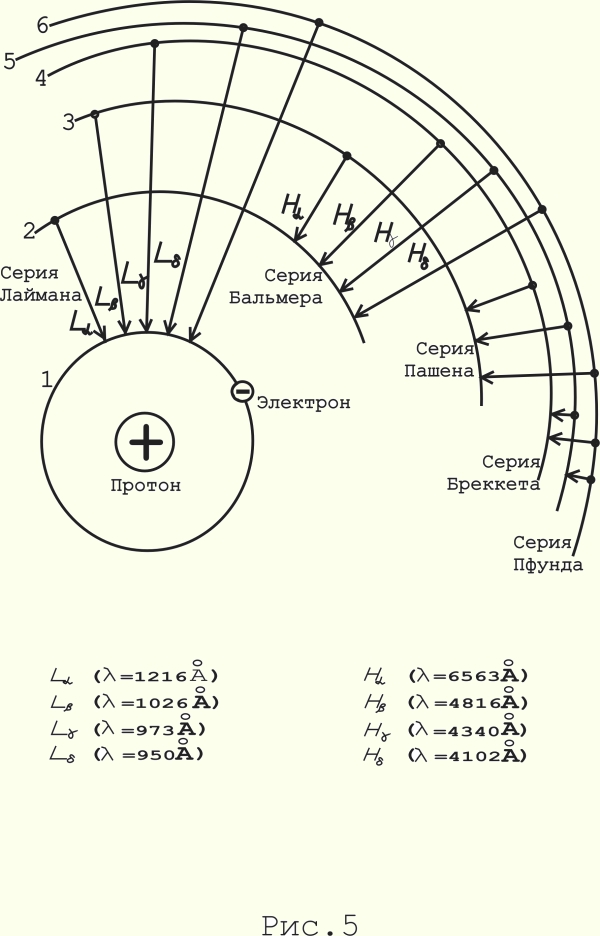
На этом рисунке схематично изображен атом водорода. Вокруг ядра /протона/ движется по круговой орбите электрон. Первая орбита /первый уровень/ - основная. Вращаясь по этой орбите, электрон не поглощает и не излучает энергию. Все остальные орбиты /уровни/ электрона /2, 3, 4, 5, 6/ - это те уровни, на которых электрон находится в возбужденном состоянии. Эти возбужденные состояния неустойчивы, и электрон стремится занять свою основную орбиту. При переходе с любой неустойчивой орбиты на основную или низшую орбиту излучается квант определенной длины волны, в зависимости от способа перехода. Эти переходы образуют серии. Например: все переходы с высших орбит на основную - серию Лаймана, переходы с орбит выше второй на вторую - серию Бальмера и т.д. Как видно из рисунка, с пятого уровня электрон может перейти на основной уровень и излучить квант длиной волны 950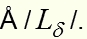
Так же электрон может перейти с пятого уровня на основной за два перехода. Сначала он перейдет на второй уровень, излучив квант длиной волны 4340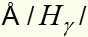 а затем со второго уровня на основной, излучив квант длиной волны 1216
а затем со второго уровня на основной, излучив квант длиной волны 1216 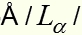 .
.
А может перейти на основной уровень за три перехода. Сначала переход из серии Пашена, затем серии Бальмера и Лаймана. Как видим, вариантов перехода с возбужденной орбиты на основную очень много. Но во всех случаях при переходах будет сохраняться одно условие – энергия поглощенного кванта основного перехода /в нашем примере /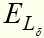 равна сумме энергий квантов промежуточных переходов /в нашем примере
равна сумме энергий квантов промежуточных переходов /в нашем примере 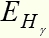 и
и 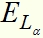 /
/
Это выразится простой формулой
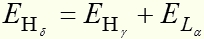 ; но
; но 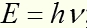 ; а т.к.
; а т.к. 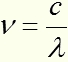
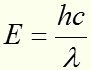
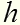 - постоянная Планка
- постоянная Планка
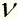 - частота кванта
- частота кванта
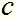 - скорость света в вакууме
- скорость света в вакууме
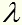 - длина волны кванта
- длина волны кванта
Это равенство примет вид
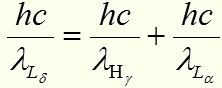 hc – выносим и сокращаем
hc – выносим и сокращаем
Получаем
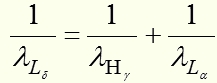
для нашего случая
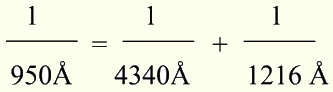
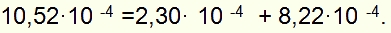
На этом примере видно, что атом водорода, поглотив квант длиной волны 950Å (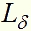 ) и перейдя в возбужденное состояние, необязательно затем переизлучит точно такой же квант. Он может переизлучить несколько квантов, сумма энергий которых равна энергии кванта, вызвавшего возбуждение.
) и перейдя в возбужденное состояние, необязательно затем переизлучит точно такой же квант. Он может переизлучить несколько квантов, сумма энергий которых равна энергии кванта, вызвавшего возбуждение.
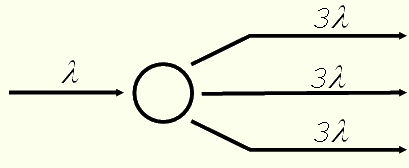
Также и мы можем наделить наш А.Пп.газ подобными свойствами. К примеру, при попадании кванта в молекулу А.Пп.газа молекула возбуждается, а при переходе в основное состояние излучит два кванта одинаковой энергии, причем сумма энергий этих двух переизлученных квантов будет равна энергии кванта, вызвавшего возбуждение молекулы А.Пп.газа.
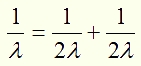
При таком равенстве мы видим, что длина волны двух переизлучен¬ных квантов удваивается. Эту схему переизлучения можно записать и в таком наглядном виде
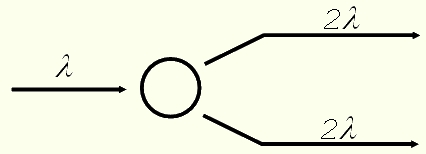
Эта схема показывает, что квант длиной волны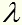 попадает в молекулу А.Пп.газа, возбуждает ее, и при переходе в невозбужденное состояние молекула излучает два кванта длиной волны 2
попадает в молекулу А.Пп.газа, возбуждает ее, и при переходе в невозбужденное состояние молекула излучает два кванта длиной волны 2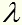 каждый.
каждый.
Можно также предположить, что при переизлучении молекулой А.Пп.газа попавшего в нее кванта образуется три кванта одинако¬вой энергии, тогда равенство запишется таким образом:
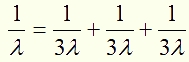
В этом случае мы видим, что длина волны 3х переизлученных квантов утраивается. Эта схема переизлучения запишется в таком виде:
А теперь представим себе, что А.Ч.тело окружено А.Пп.газом с вышеизложенными свойствами. Не трудно догадаться, что даже если А.Ч.тело нагрето до нескольких миллионов градусов и максимум его излучения приходится на кванты рентгеновского диапазона, то при достаточном количестве переизлучений в среде А.Пп. газа, обладающего вышеизложенными свойствами, мы квантов рентгеновского диапазона почти не зарегистрируем, а максимум излучения придет, например, на кванты видимого диапазона и радиоволны. Конечно, какую-то мизерную часть квантов рентгеновского диапазона мы зарегистрируем. Это те кванты, которые прошли сквозь всю толщу атмосферы А.Пп. газа, так ни разу не попав в его молекулу, а, следовательно, так ни разу и не переизлучившись.
На основании вышеприведенных выкладок сформируем общие положения излучения А.Ч.тела в среде А.Пп.газа.
1. Если А.Ч.тело излучает свою энергию в среде какого-то реального газа, то надо знать насколько свойства этого реального газа приближаются к свойствам А.Пп.газа.
2. Если реальный газ, окружающий А.Ч.тело способен переизлучать кванты высокой энергии по схемам
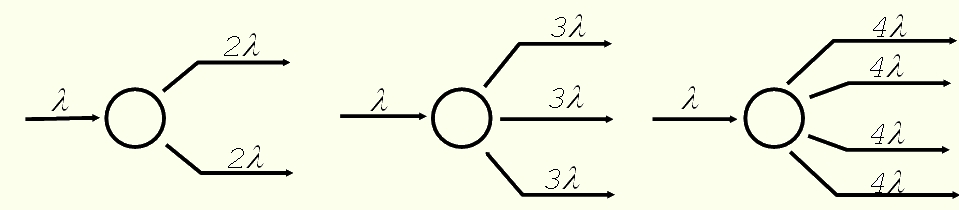
и т. д., то пренебрежение этими свойствами реального газа ведет к ошибке определения истинной температуры поверхности А.Ч.тела.
3. Не зная среднего количества переизлучений К первоначально излученного поверхностью А.Ч.тела кванта, нельзя даже приблизительно говорить о величине первоначально излученной А.Ч.телом энергии.
4. Если А.Ч.тело излучает свою энергию в вакууме, то только в этом случае можно применять в чистом виде законы Планка, Стефана - Больцмана и Вина для определения температуры А.Ч.тела.
После того, как мы сформулировали эти четыре основных положения излучения А.Ч.тела в среде А.Пп.газа, мы уже по-другому рассмотрим процессы, протекающие на Солнце. Если раньше мы принадлежали к экспериментаторам категории Б, то теперь принадлежим к экспериментаторам категории А, т.е., тем экспериментаторам, которые имеют представление о процессах переизлучения квантов в среде А.Пп.газа.
Возьмем А.Ч. тело радиусом r и нагреем его до температуры T. В начале нашего эксперимента А.Ч. тело /радиуса r и температуры T/ поместим в вакуум и на расстоянии R от центра А.Ч. тела измерим болометрическим датчиком то количество энергии E, которое попадет на единицу поверхности в единицу времени. Полная энергия, излученная А.Ч. телом за единицу времени в окружающее пространство, будет:
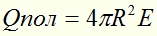
Т.к. площадь поверхности А.Ч. тела равна
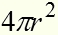 , то энергия, излучаемая единицей площади А.Ч. тела в единицу времени, будет:
, то энергия, излучаемая единицей площади А.Ч. тела в единицу времени, будет: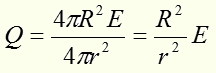
Применяя закон Стефана-Больцмана, измерим температуру А.Ч. тела

Подставляя значение
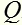 в формулу /2/, получаем температуру T
в формулу /2/, получаем температуру T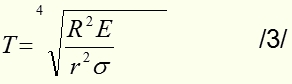
Видоизменим опыт. Пространство на расстоянии R от центра А.Ч. тела заполним А.Пп. газом и посмотрим, какую энергию зарегистрирует болометрический датчик в этом случае. /Расстояние от центра А.Ч.тела до болометрического датчика неизменно остается R/. Но теперь нам надо знать, каково будет среднее количество переизлучений квантов, излученных А.Ч. телом. Каким-то образом нам удалось зарегистрировать среднее количество переизлучений K первоначально излученных квантов в среде А.Пп. газа. Тогда болометрический датчик зарегистрирует энергию в
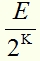
А теперь представим, что эти данные, полученные по показа¬ниям болометрического датчика /болометрических датчиков/, используют в своих исследованиях два экспериментатора, А и Б.
Экспериментатор А знает, что А.Ч. тело окружено А.Пп. газом, а также знает, каким образом А.Ч. тело излучает свою энергию в среде А.Пп. газа.
Экспериментатор Б знает, что А.Ч. тело окружено каким-то газом, но он считает, что этот газ почти не влияет на величину энергии излучения А.Ч. тела. А если как-то влияет, то этой величиной, вследствие того, что она мала /он так думает/, можно пренебречь. Т.е. экспериментатор Б пользуется только законами Планка, Стефана-Больцмана, Вина для излучения А.Ч. тела в вакууме.
Представим себе, что оба экспериментатора снабжены несколькими болометрическими датчиками, регистрирующими энергию квантов во всем диапазоне длин волн, излучаемых А.Ч. телом. Т.е. при помощи этих болометрических датчиков экспериментаторы смогут построить кривую распределения энергии, излучаемой А.Ч. телом в зависимости от длины волны. У обоих экспериментаторов есть прибор угломер. При помощи этого прибора они смогут точно определить угол, под которым наблюдается поверхность А.Ч. тела, а следовательно зная R, могут определить r.
Экспериментатор А начнет с того, что по показаниям болометрических датчиков построит кривую распределения энергии, излучаемой А.Ч. телом в зависимости от длины волны /сплошная кривая см. рис, 4/. Далее из построенного графика он определит максимум этой кривой и найдет λmах. Затем, применив закон Вина Tλmах=2896 мк*град., экспериментатор А определит истинную температуру А.Ч. тела:

После этого по формуле /З/ экспериментатор А определит ту суммарную энергию, которую должны были бы зарегистрировать его болометрические датчики, если бы А.Ч.тело излучало в вакууме.
Подставляя /4/, получаем:
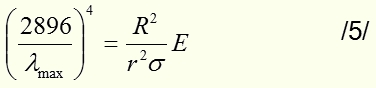
отсюда:
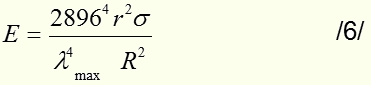
где E - суммарная энергия на единицу площади, которую должны были бы зарегистрировать болометрические датчики, если бы А.Ч. тело излучало в вакууме.
Но болометрические датчики зарегистрировали энергию в
Сравнивая величины
Посмотрим, как экспериментатор Б справится с задачей. Все ли у него получится в соответствии с данными эксперимента.
В начале экспериментатор Б поступит так же, как и А. По показаниям болометрических датчиков он построит кривую распределения энергии, излучаемой А.Ч. телом в зависимости от длины волны /сплошная кривая см. рис. 4/. Далее, определив λmах, он по формуле Вина определит температуру Т А.Ч. тела.

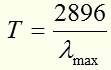
Затем экспериментатор Б решит проверить эти данные температуры по формуле Стефана-Больцмана. Суммарная энергия на единицу поверхности, которую зарегистрируют его болометрические датчики, будет равна
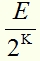
Экспериментатор Б обнаружит, что величина в правой части равенства будет меньше, чем в левой части. И чем больше будет величина K, тем большее несоответствие правой и левой частей уравнения обнаружит экспериментатор Б. Возможно, экспериментатор Б решит, что радиус А.Ч. тела был определен
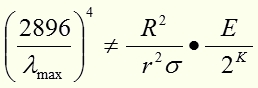
неправильно. А возможно, экспериментатор Б решит, что разница в левой и правой частях уравнения объясняется погрешностью измерения болометрических датчиков. Но применяя более точные приборы, экспериментатор Б придет к тем же необъяснимым результатам.
На основании вышеизложенного примера с экспериментаторами А и Б читатель убедился в том, что если А.Ч. тело излучает свою энергию не в вакууме, а в среде какого-то газа, то надо знать, насколько свойства реального газа, окружающего А.Ч.тело, приближаются к свойствам А.Пп. газа. Пренебрежение свойствами А.Пп. газа может привести к большим ошибкам в исследовании экс-периментальных данных, в чем вы убедились.
Был разобран простейший случай переизлучения А.Пп. газом квантов по всему спектру излучения А.Ч. тела, когда попавший в молекулу А.Пп. газа квант переизлучился в точно такой же квант. Но, как известно, в природе существует и более сложный способ переизлучения. Для примера обратимся к спектру атома водорода /см. рис.5/.

На этом рисунке схематично изображен атом водорода. Вокруг ядра /протона/ движется по круговой орбите электрон. Первая орбита /первый уровень/ - основная. Вращаясь по этой орбите, электрон не поглощает и не излучает энергию. Все остальные орбиты /уровни/ электрона /2, 3, 4, 5, 6/ - это те уровни, на которых электрон находится в возбужденном состоянии. Эти возбужденные состояния неустойчивы, и электрон стремится занять свою основную орбиту. При переходе с любой неустойчивой орбиты на основную или низшую орбиту излучается квант определенной длины волны, в зависимости от способа перехода. Эти переходы образуют серии. Например: все переходы с высших орбит на основную - серию Лаймана, переходы с орбит выше второй на вторую - серию Бальмера и т.д. Как видно из рисунка, с пятого уровня электрон может перейти на основной уровень и излучить квант длиной волны 950
Так же электрон может перейти с пятого уровня на основной за два перехода. Сначала он перейдет на второй уровень, излучив квант длиной волны 4340
А может перейти на основной уровень за три перехода. Сначала переход из серии Пашена, затем серии Бальмера и Лаймана. Как видим, вариантов перехода с возбужденной орбиты на основную очень много. Но во всех случаях при переходах будет сохраняться одно условие – энергия поглощенного кванта основного перехода /в нашем примере /
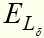 равна сумме энергий квантов промежуточных переходов /в нашем примере
равна сумме энергий квантов промежуточных переходов /в нашем примере 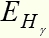 и
и 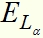 /
/Это выразится простой формулой
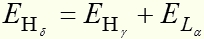 ; но
; но 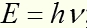 ; а т.к.
; а т.к. 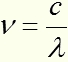
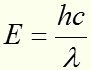
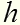 - постоянная Планка
- постоянная Планка 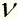 - частота кванта
- частота кванта 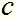 - скорость света в вакууме
- скорость света в вакууме 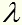 - длина волны кванта
- длина волны квантаЭто равенство примет вид
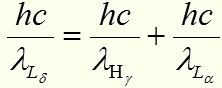 hc – выносим и сокращаем
hc – выносим и сокращаемПолучаем
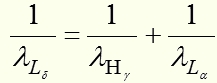
для нашего случая
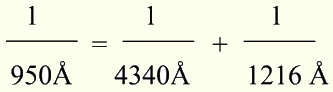
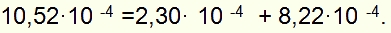
На этом примере видно, что атом водорода, поглотив квант длиной волны 950Å (
 ) и перейдя в возбужденное состояние, необязательно затем переизлучит точно такой же квант. Он может переизлучить несколько квантов, сумма энергий которых равна энергии кванта, вызвавшего возбуждение.
) и перейдя в возбужденное состояние, необязательно затем переизлучит точно такой же квант. Он может переизлучить несколько квантов, сумма энергий которых равна энергии кванта, вызвавшего возбуждение.Также и мы можем наделить наш А.Пп.газ подобными свойствами. К примеру, при попадании кванта в молекулу А.Пп.газа молекула возбуждается, а при переходе в основное состояние излучит два кванта одинаковой энергии, причем сумма энергий этих двух переизлученных квантов будет равна энергии кванта, вызвавшего возбуждение молекулы А.Пп.газа.
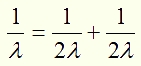
При таком равенстве мы видим, что длина волны двух переизлучен¬ных квантов удваивается. Эту схему переизлучения можно записать и в таком наглядном виде

Эта схема показывает, что квант длиной волны
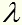 попадает в молекулу А.Пп.газа, возбуждает ее, и при переходе в невозбужденное состояние молекула излучает два кванта длиной волны 2
попадает в молекулу А.Пп.газа, возбуждает ее, и при переходе в невозбужденное состояние молекула излучает два кванта длиной волны 2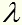 каждый.
каждый.Можно также предположить, что при переизлучении молекулой А.Пп.газа попавшего в нее кванта образуется три кванта одинако¬вой энергии, тогда равенство запишется таким образом:
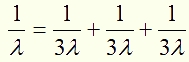
В этом случае мы видим, что длина волны 3х переизлученных квантов утраивается. Эта схема переизлучения запишется в таком виде:

А теперь представим себе, что А.Ч.тело окружено А.Пп.газом с вышеизложенными свойствами. Не трудно догадаться, что даже если А.Ч.тело нагрето до нескольких миллионов градусов и максимум его излучения приходится на кванты рентгеновского диапазона, то при достаточном количестве переизлучений в среде А.Пп. газа, обладающего вышеизложенными свойствами, мы квантов рентгеновского диапазона почти не зарегистрируем, а максимум излучения придет, например, на кванты видимого диапазона и радиоволны. Конечно, какую-то мизерную часть квантов рентгеновского диапазона мы зарегистрируем. Это те кванты, которые прошли сквозь всю толщу атмосферы А.Пп. газа, так ни разу не попав в его молекулу, а, следовательно, так ни разу и не переизлучившись.
На основании вышеприведенных выкладок сформируем общие положения излучения А.Ч.тела в среде А.Пп.газа.
1. Если А.Ч.тело излучает свою энергию в среде какого-то реального газа, то надо знать насколько свойства этого реального газа приближаются к свойствам А.Пп.газа.
2. Если реальный газ, окружающий А.Ч.тело способен переизлучать кванты высокой энергии по схемам

и т. д., то пренебрежение этими свойствами реального газа ведет к ошибке определения истинной температуры поверхности А.Ч.тела.
3. Не зная среднего количества переизлучений К первоначально излученного поверхностью А.Ч.тела кванта, нельзя даже приблизительно говорить о величине первоначально излученной А.Ч.телом энергии.
4. Если А.Ч.тело излучает свою энергию в вакууме, то только в этом случае можно применять в чистом виде законы Планка, Стефана - Больцмана и Вина для определения температуры А.Ч.тела.
После того, как мы сформулировали эти четыре основных положения излучения А.Ч.тела в среде А.Пп.газа, мы уже по-другому рассмотрим процессы, протекающие на Солнце. Если раньше мы принадлежали к экспериментаторам категории Б, то теперь принадлежим к экспериментаторам категории А, т.е., тем экспериментаторам, которые имеют представление о процессах переизлучения квантов в среде А.Пп.газа.